Chi-square distribution¶

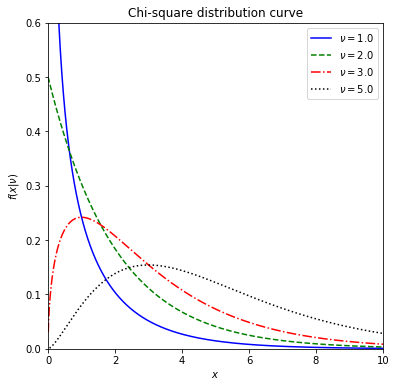
Let’s investigate how shape of the chisquare distribution curve look likes.

# import required libraries
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from IPython.display import display

Let’s now investigate how shape of the chi-square distribution curve changes with respect to degrees of freedom (\(\nu\)). We will define a function first to simplify our calculations.

# define a Python function with three parameters

def chi2_dist_curve(dof, ltype, col):
    
    fig, ax = plt.subplots(figsize = (6, 6))
    
    #use zip for parallel iteration
    for d, l, cl in zip(dof, ltype, col):
        #generate 10000 random variables for given degrees of freedom
        x = stats.chi2.rvs(df = d, size = 10000)
        x1 = np.sort(x)
        plt.plot(x1, stats.chi2.pdf(x1, df = d), 
                 ls = l, c = cl, label = r'$\nu=%.1f$' % (d))  
        
    plt.xlim(0, 10) #change as needed
    plt.ylim(0, 0.6) #change as needed
    plt.xlabel('$x$')
    plt.ylabel(r'$f(x|\nu)$')
    plt.title('Chi-square distribution curve')
    plt.legend(loc='upper right')
    plt.show()

Now play with the function to see the changes on the normal distribution curve.

## change the following values as you wish
## define the input arguments (values of the parameters)
dof_values = [1, 2, 3, 5]
linestyles = ['-', '--', '-.', ':']
colors = ['blue', 'green','red','black']

chi2_curve = chi2_dist_curve(dof = dof_values, ltype = linestyles, col = colors)

display(chi2_curve)

None

Calculate probabilities associated with chi-square distribution with ‘stats.chi2.cdf(x, df)’.

#example in class
# x follows a chi-square with 5 dof
prob_int = stats.chi2.cdf(x = 12.83, df = 5) - stats.chi2.cdf(x = 1.145, df = 5)
print("%.4f"%prob_int)

0.9250

Spring 2022

Chi-square distribution

Chi-square distribution¶